Forschung
Primzahlzwillings-Rekorde
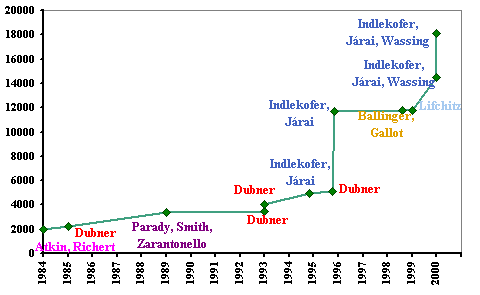
Die Suche nach den größten bekannten Primzahlzwillingspaaren
- Ausgangspunkt der Suche waren die arithmetischen Progressionen (5775 +
30030h)·260000 ± 1, wobei der
Exponent 60.000 fest war und h alle Zahlen von 0 bis 227
= 134.217.738 durchlaufen konnte.
- Beide Progressionen wurden durch die Primzahlen zwischen 7 und 241=
2.199.023.255.552 gesiebt. Dieser Prozeß dauerte ca 50 CPU-Tage. Nach
dem Sieben blieben 280.186 Kandidaten übrig.
- Auf die verbliebenen Kandidaten wurde der probabilistische Test von
Miller-Rabin angewandt, zuerst für den Fall –1, danach für +1.
Bereits nach den ersten 65.000 Tests wurde ein "wahrscheinlicher"
Primzahlzwilling gefunden. Die für einen Test benötigte CPU-Zeit
betrug ca. 4,3 Minuten bei einer Zyklusgeschwindigkeit von 400 MHz.
Für den Test wurden maximal 50 UltraSPARC CPU mit Taktfrequenzen zwischen 140
und 400 MHz benutzt.
- Der "wahrscheinliche" Primzahlzwilling (2.409.110.779.845)·260000
± 1 (mit 18.075 Dezimalstellen) wurde durch exakte Verfahren untersucht: der Fall –1
mit Hilfe des Lucas-Tests, der Fall +1 durch den Test von Brillhart, Lehmer
und Selfridge.
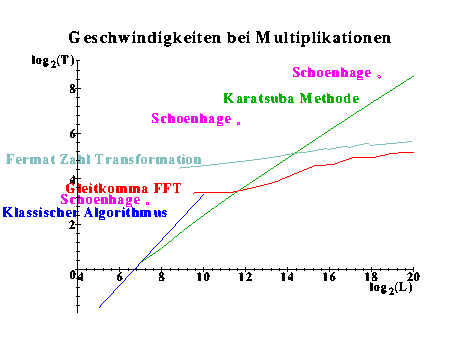
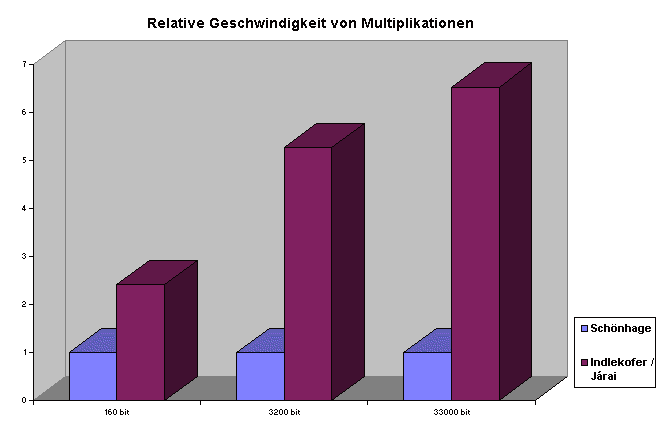
Die Geschwindigkeit der Primzahltests wird durch die Leistungsfähigkeit
der Multiplikation bestimmt. Die einzelnen Multiplikationsmethoden sind
jeweils in verschiedenen Ziffernlängen-Bereichen optimal. Die obige
Darstellung zeigt die Leistungsfähigkeit unserer Programme. Hierbei
wird die Anzahl T der benötigten Takte/bit in Abhängigkeit von
der binären Ziffernanzahl L ausgedrückt. Zum Vergleich sind einige
von Schönhage et. al. (Bonn) erzielte Ergebnisse angegeben.
Literatur
-
K.-H. Indlekofer, A.
Járai, Largest known twin primes, Math. Comp. 65(1996),
427-428. MR 96d:11009
-
K.-H. Indlekofer, A.
Járai, Some world records in computational number theory,
Leaflets in Mathematics, Janus Pannonius University, Pécs,
6(1998), 49-56, ISSN 1416-0935
-
K.-H. Indlekofer, A.
Járai, Largest known twin primes and Sophie Germain primes,
Math. Comp. 68(1999), 1317-1324. MR 99k:11013
|